Apa itu K-Means Clustering

Definisi K-Means Clustering

K-Means Clustering adalah algoritma unsupervised learning yang digunakan untuk mengelompokkan data ke dalam K kelompok (cluster) berdasarkan kemiripan atau jarak tertentu. Algoritma ini berupaya meminimalkan jumlah kuadrat jarak antara data dalam satu cluster dengan centroidnya. Metode ini sering digunakan dalam analisis data eksploratif untuk menemukan pola tersembunyi di dalam dataset.

Cara Kerja K-Means

Tentukan jumlah cluster K.
Inisialisasi centroid secara acak sebanyak K.
Hitung jarak setiap data ke centroid dan tetapkan data ke cluster dengan jarak terdekat.
Perbarui posisi centroid dengan menghitung rata-rata posisi data dalam masing-masing cluster.
Ulangi langkah 3 dan 4 hingga centroid tidak berubah atau perubahan nilai sangat kecil.

Proses ini dikenal sebagai iterasi ulang-alik (iterative refinement) yang secara bertahap mengurangi nilai fungsi objektif hingga konvergen.

Rumus-Rumus yang Berkaitan

Jarak Euclidean: \( d(x, c) = \sqrt{\sum_{i=1}^n (x_i - c_i)^2} \)
Update Centroid: \( c_j = \frac{1}{|S_j|} \sum_{x \in S_j} x \)
Fungsi Objektif: \( J = \sum_{j=1}^K \sum_{x \in S_j} \|x - c_j\|^2 \)

Contoh Soal K-Means

Soal:

Diberikan dataset berikut dengan dua fitur (X1 dan X2):

            
Data:
+-------+------+------+  
| Index | X1   | X2   |  
+-------+------+------+
| 1     | 1.0  | 1.0  |  
| 2     | 1.5  | 2.0  |  
| 3     | 3.0  | 4.0  |  
| 4     | 5.0  | 7.0  |  
| 5     | 3.5  | 5.0  |  
| 6     | 4.5  | 5.0  |  
| 7     | 3.5  | 4.5  |  
+-------+------+------+

Lakukan clustering dengan K=2. Centroid awal adalah (1.0, 1.0) dan (5.0, 7.0).

Penyelesaian:

Langkah 1: Hitung jarak setiap titik ke centroid

Gunakan rumus jarak Euclidean:

\( d(x, c) = \sqrt{(x_1 - c_1)^2 + (x_2 - c_2)^2} \)

Centroid awal:

Centroid 1: (1.0, 1.0)
Centroid 2: (5.0, 7.0)

Perhitungan jarak:

Data	Ke Centroid 1	Ke Centroid 2	Cluster
(1.0, 1.0)	0	7.21	1
(1.5, 2.0)	1.12	6.50	1
(3.0, 4.0)	3.61	4.72	1
(5.0, 7.0)	7.21	0	2
(3.5, 5.0)	5.31	2.50	2
(4.5, 5.0)	6.40	2.24	2
(3.5, 4.5)	5.31	2.69	2

Langkah 2: Perbarui centroid
Hitung rata-rata posisi data dalam setiap cluster:
- Centroid 1: Rata-rata dari (1.0, 1.0), (1.5, 2.0), dan (3.0, 4.0)
- Centroid baru: \(( \frac{1.0 + 1.5 + 3.0}{3}, \frac{1.0 + 2.0 + 4.0}{3} ) = (1.83, 2.33)\)
- Centroid 2: Rata-rata dari (5.0, 7.0), (3.5, 5.0), (4.5, 5.0), dan (3.5, 4.5)
- Centroid baru: \(( \frac{5.0 + 3.5 + 4.5 + 3.5}{4}, \frac{7.0 + 5.0 + 5.0 + 4.5}{4} ) = (4.13, 5.38)\)
Langkah 3: Ulangi langkah 1 dan 2 hingga konvergen
Proses ini dilanjutkan hingga centroid tidak lagi berubah signifikan.

Keuntungan dan Penerapan

Keuntungan

Mudah diimplementasikan dan cepat untuk dataset kecil hingga sedang.
Efisien untuk data yang memiliki cluster dengan bentuk bulat.

Kerugian

Sensitif terhadap inisialisasi centroid awal, yang dapat menghasilkan solusi lokal yang kurang optimal.
Kesulitan dalam menangani data yang memiliki ukuran cluster berbeda atau distribusi yang tidak bulat.
Sensitif terhadap outlier, yang dapat memengaruhi posisi centroid secara signifikan.
Memerlukan pengguna untuk menentukan jumlah cluster K sebelum proses clustering dimulai.

Kapan Digunakan

K-Means digunakan ketika ingin mengelompokkan data ke dalam sejumlah cluster yang telah ditentukan sebelumnya, terutama jika data memiliki dimensi rendah hingga sedang. Algoritma ini sering digunakan dalam analisis segmentasi pasar, pengelompokan gambar, dan reduksi data.

Implementasi K-Means dalam Python

Berikut adalah contoh implementasi sederhana K-Means menggunakan library scikit-learn:

1. Persiapan Data

Tutorial kali ini kita menggunaka dataset iris untuk melakukan klasifikasi.


# Import library yang diperlukan
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score, homogeneity_score, completeness_score, v_measure_score
from sklearn.datasets import load_iris

# Memuat dataset Iris
iris = load_iris()
data = iris.data  # Fitur dataset
true_labels = iris.target  # Label asli untuk evaluasi
feature_names = iris.feature_names

# Mengubah dataset menjadi DataFrame
df = pd.DataFrame(data, columns=feature_names)
print(df.head)

2. Menentukan Jumlah Cluster (K)

Ada beberapa metode untuk menentukan jumlah cluster (K) yang optimal. Dua metode yang sering digunakan adalah:

Elbow Method
Silhouette Score

Elbow Method

Metode ini melibatkan plotting dari jumlah cluster (K) yang berbeda dengan nilai "inertia" atau SSE (Sum of Squared Errors) untuk setiap nilai K, dan mencari titik elbow (titik yang mulai melandai).


# Menentukan range K yang akan diuji
n_samples = len(df)
k_range = range(1, min(11, n_samples + 1)) 

# Menghitung inertia untuk setiap nilai K
inertia = []
for k in k_range:
    kmeans = KMeans(n_clusters=k, random_state=42)
    kmeans.fit(df)
    inertia.append(kmeans.inertia_)

# Plot Metode Elbow
plt.figure(figsize=(8, 5))
plt.plot(k_range, inertia, marker='o', linestyle='--')
plt.title('Metode Elbow untuk Menentukan Jumlah Cluster Optimal')
plt.xlabel('Jumlah Cluster (K)')
plt.ylabel('Inertia')
plt.show()

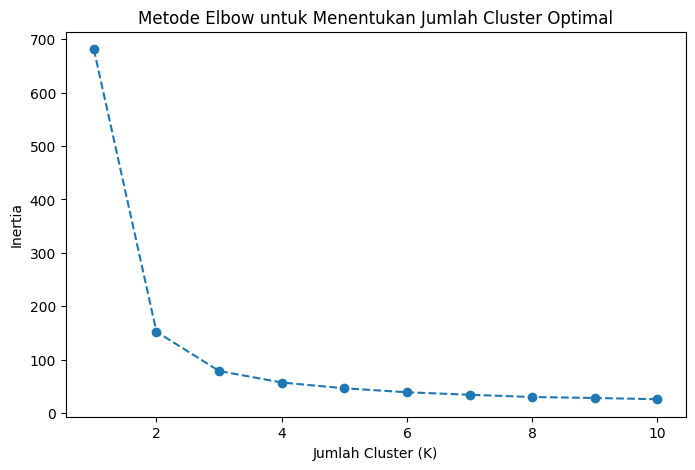
Berdasarkan grafik Elbow, kita mendapatkan nilai 𝐾=3 karena pada titik tersebut grafik mulai melandai, atau SSE (Sum of Squared Errors) mulai tidak menunjukkan penurunan yang terlalu ekstrim.

3. Melakukan K-Means dengan K Optimal

Setelah menentukan K yang optimal menggunakan Elbow Method atau Silhouette Score, kita dapat melanjutkan untuk melakukan clustering.


# Menentukan jumlah cluster optimal berdasarkan analisis Elbow
optimal_k = 3  # Sesuai grafik elbow

kmeans = KMeans(n_clusters=optimal_k, random_state=42)
kmeans.fit(df)

# Menambahkan hasil cluster ke DataFrame
df['Cluster'] = kmeans.labels_

4. Visualisasi


# Visualisasi hasil clustering (menggunakan dua fitur pertama untuk scatter plot)
plt.figure(figsize=(8, 5))
plt.scatter(
    df[feature_names[0]],  # Sepal length (cm)
    df[feature_names[1]],  # Sepal width (cm)
    c=df['Cluster'],
    cmap='viridis',
    alpha=0.6,
    edgecolor='k'
)
plt.scatter(
    kmeans.cluster_centers_[:, 0],  # Centroid untuk fitur pertama
    kmeans.cluster_centers_[:, 1],  # Centroid untuk fitur kedua
    s=200,
    c='red',
    marker='X',
    label='Cluster Centers'
)
plt.title('Hasil Clustering dengan K-Means (Dataset Iris)')
plt.xlabel(feature_names[0])
plt.ylabel(feature_names[1])
plt.legend()
plt.show()

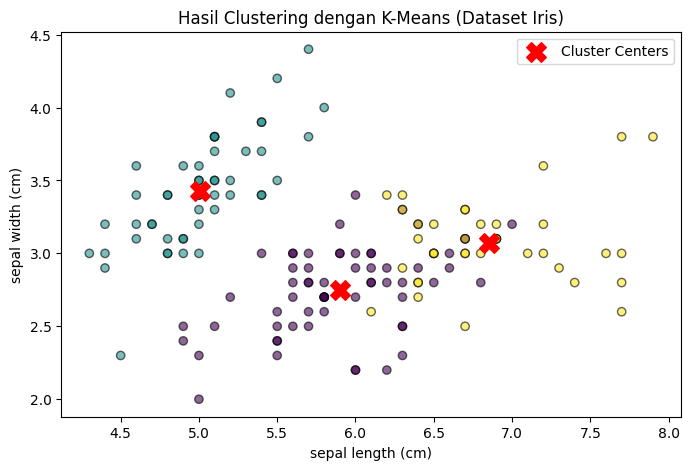
5. Evaluasi Model

Jika kita tahu nilai sebenarnya dari label cluster (misalnya, jika ini adalah tugas semi-supervised), kita bisa mengevaluasi model menggunakan metrik seperti Homogeneity, Completeness, dan V-Measure. Namun, dalam clustering unsupervised, metrik ini sering tidak tersedia.


# Evaluasi model menggunakan Homogeneity, Completeness, dan V-Measure
print(f"Homogeneity: {homogeneity_score(true_labels, kmeans.labels_):.2f}")
print(f"Completeness: {completeness_score(true_labels, kmeans.labels_):.2f}")
print(f"V-Measure: {v_measure_score(true_labels, kmeans.labels_):.2f}")

# Evaluasi Silhouette Score untuk K optimal
silhouette_avg = silhouette_score(df.iloc[:, :-1], kmeans.labels_)
print(f"Silhouette Score untuk K={optimal_k}: {silhouette_avg:.2f}")

Homogeneity: 0.75; mengukur seberapa seragam klaster-klaster dalam hal label mereka. Nilai 0.75 menunjukkan bahwa kebanyakan titik data dalam setiap klaster memiliki label yang sama. Meskipun bukan nilai sempurna, ini menunjukkan bahwa klaster yang dihasilkan cukup baik dalam mengelompokkan data berdasarkan label yang seragam.
Completeness:0.76; mengukur seberapa baik anggota dengan label yang sama ditempatkan dalam klaster yang sama. Nilai 0.76 menunjukkan bahwa kebanyakan titik data dengan label yang sama ditemukan dalam klaster yang sama. Ini menunjukkan kemampuan klaster untuk menyatukan data dengan label yang sama ke dalam satu grup.
V-Measure:0.76; adalah rata-rata harmonis dari homogeneity dan completeness. Nilai 0.76 menunjukkan keseimbangan yang baik antara keduanya. Dengan kata lain, klaster yang dihasilkan cukup konsisten dalam hal keseragaman dan kelengkapan label.