Ngobrolin Margin of Error, Standard Error, & Confidence Interval: Biar Nggak Asal Nge-Analisis!
Sumber: Wikipedia
Pendahuluan
Halo teman-teman MathAlpha! 👋 Pernah lihat hasil survei yang bilang kayak gini: "Tingkat kepuasan 70% dengan margin of error ±3%"? Nah, angka ±3% itu bukan tempelan doang ya. Itu namanya Margin of Error (MoE), dan dia bagian dari trio statistik keren bareng Standard Error dan Confidence Interval.
Ketiga istilah ini penting banget buat ngerti seberapa akurat hasil survei atau penelitian. Yuk mimin ajak bahas satu-satu, dengan gaya santai tapi tetap berbobot! 📊✨
Apa itu Margin of Error?
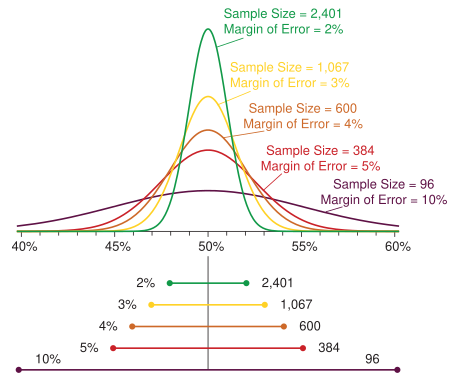
Margin of Error (MoE) itu semacam “batas toleransi” dari hasil survei kamu. Jadi misalnya kamu dapet hasil survei bahwa 70% orang suka es kopi, terus MoE-nya ±3%, artinya hasil aslinya bisa aja antara 67% sampai 73%.
Kenapa bisa beda? Karena kita cuma ngambil sampel dari populasi, bukan seluruh orang di dunia. Jadi, ya pasti ada potensi meleset dikit. Nah, MoE ini yang bantu kita ukur seberapa besar kemungkinan melesetnya.
Rumus Margin of Error
Margin of error dapat dihitung menggunakan rumus berikut:
\[ MoE = Z \times SE \]
Dimana:
- \(Z\): Z-score yang sesuai dengan tingkat kepercayaan (misalnya, 1.96 untuk tingkat kepercayaan 95%).
- \(SE\): Standard Error.
Contoh Perhitungan
Misalkan:
- Standard error (SE) = 2
- Z-score untuk tingkat kepercayaan 95% = 1.96
Maka margin of error adalah:
\[ MoE = 1.96 \times 2 = 3.92 \]
Interpretasi: Dengan tingkat kepercayaan 95%, parameter populasi diperkirakan berada dalam rentang nilai sampel ±3.92. Artinya, jika rata-rata sampel adalah 50, maka rata-rata populasi diperkirakan berada antara 46.08 hingga 53.92.
Apa itu Standard Error?
Oke, sekarang kita ke Standard Error (SE). Ini tuh kayak ngukur seberapa ‘goyang’ rata-rata dari sampel kita terhadap nilai asli dari populasi.
Makin kecil SE-nya, makin deket hasil kita sama populasi sebenarnya. SE juga tergantung ukuran sampel dan sebaran data. Jadi, makin banyak data, makin kecil SE-nya.
Rumus Standard Error
Untuk rata-rata sampel, standard error dihitung sebagai:
\[ SE = \frac{\sigma}{\sqrt{n}} \]
Dimana:
- \(\sigma\): Simpangan baku populasi.
- \(n\): Ukuran sampel.
Contoh Perhitungan
Misalkan simpangan baku populasi adalah 10 dan ukuran sampel adalah 25:
\[ SE = \frac{10}{\sqrt{25}} = 2 \]
Interpretasi: Variabilitas rata-rata sampel diperkirakan ±2 unit dari rata-rata populasi. Artinya, jika rata-rata populasi adalah 50, rata-rata sampel dapat bervariasi antara 48 hingga 52.
Apa itu Confidence Interval?
Nah ini dia, si Confidence Interval (CI). Ini adalah rentang nilai yang punya kemungkinan besar (misalnya 95%) mencakup nilai asli dari populasi.
Confidence interval sering digunakan dalam penelitian untuk memberikan estimasi yang lebih akurat tentang parameter populasi. Semakin lebar interval, semakin besar ketidakpastian, dan semakin sempit interval, semakin tinggi tingkat kepercayaan kita terhadap estimasi tersebut.
Rumus Confidence Interval
Confidence interval dihitung sebagai:
\[ CI = \bar{x} \pm MoE \]
Dimana:
- \(\bar{x}\): Nilai rata-rata sampel.
- MoE: Margin of Error.
Contoh Perhitungan
Misalkan rata-rata sampel adalah 50, dan margin of error adalah 3.92:
\[ CI = 50 \pm 3.92 = (46.08, 53.92) \]
Interpretasi: Dengan tingkat keyakinan 95%, parameter populasi diperkirakan berada dalam rentang 46.08 hingga 53.92. Artinya, ada kemungkinan sebesar 95% bahwa rata-rata populasi benar-benar berada di antara nilai tersebut.
Hubungan Ketiganya
-
Standard Error itu dasar dari semuanya – ngukur seberapa "acak" data kamu.
-
Dari SE, kamu bisa hitung Margin of Error.
-
Dari MoE, kamu bisa bikin Confidence Interval.
Kalau ukuran sampel diperbesar ➜ SE makin kecil ➜ MoE makin kecil ➜ CI makin sempit ➜ hasil analisis makin presisi! 🎯
Kesimpulan
Margin of Error, Standard Error, dan Confidence Interval adalah konsep-konsep penting dalam statistika yang membantu kita memahami seberapa akurat hasil sampel dapat menggambarkan populasi sebenarnya. Dengan memahami cara menghitung dan menginterpretasikan ketiga konsep ini, kita dapat membuat kesimpulan yang lebih tepat dan informatif dari data yang kita miliki.
Semoga artikel ini membantu Anda memahami lebih dalam tentang ketiga konsep tersebut.